

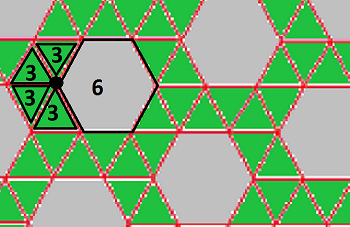
Tessellation is when you put shapes together to create a pattern without gaps between the shapes. However, that’s very narrow, and doesn’t capture the breadth of meaning of tessellations in math, nature, and design.
The dictionary definition of tessellations is to arrange in a mosaic pattern.
TESSELLATION MATH DEFINITION HOW TO
Here, we introduce this fun type of pattern and guide you through how to make tessellations. Tessellations can use simple geometric shapes (such as squares and triangles) or much more complex or irregular shapes (such as stylized birds or fish) that have been designed to fit together neatly in a repeating pattern.
There is no reflectional symmetry, nor is there rotational symmetry.Ī pentomino is the shape of five connected checkerboard squares.A tessellation pattern is one composed of shapes without gaps or overlaps. In glide reflection, reflection and translation are used concurrently much like the following piece by Escher, Horseman. A rotation, or turn, occurs when an object is moved in a circular fashion around a central point which does not move.Ī good example of a rotation is one "wing" of a pinwheel which turns around the center point. Rotations always have a center, and an angle of rotation. Rotation is spinning the pattern around a point, rotating it. To reflect a shape across an axis is to plot a special corresponding point for every point in the original shape. If a reflection has been done correctly, you can draw an imaginary line right through the middle, and the two parts will be symmetrical "mirror" images. Most commonly flipped directly to the left or right (over a "y" axis) or flipped to the top or bottom (over an "x" axis), reflections can also be done at an angle. The translation shows the geometric shape in the same alignment as the original it does not turn or flip.Ī reflection is a shape that has been flipped. These were described by Escher.Ī translation is a shape that is simply translated, or slid, across the paper and drawn again in another place. There are 4 ways of moving a motif to another position in the pattern. He adopted a highly mathematical approach with a systematic study using a notation which he invented himself. There are 17 possible ways that a pattern can be used to tile a flat surface or 'wallpaper'.Įscher read Pólya's 1924 paper on plane symmetry groups.Escher understood the 17 plane symmetry groups described in the mathematician Pólya's paper, even though he didn't understand the abstract concept of the groups discussed in the paper.īetween 19 Escher produced 43 colored drawings with a wide variety of symmetry types while working on possible periodic tilings. One mathematical idea that can be emphasized through tessellations is symmetry. If you look at a completed tessellation, you will see the original motif repeats in a pattern.

The term has become more specialised and is often used to refer to pictures or tiles, mostly in the form of animals and other life forms, which cover the surface of a plane in a symmetrical way without overlapping or leaving gaps. They were used to make up 'tessellata' - the mosaic pictures forming floors and tilings in Roman buildings The word 'tessera' in latin means a small stone cube. When you fit individual tiles together with no gaps or overlaps to fill a flat space like a ceiling, wall, or floor, you have a tiling. A tessellation is created when a shape is repeated over and over again covering a plane without any gaps or overlaps.Īnother word for a tessellation is a tiling.


 0 kommentar(er)
0 kommentar(er)
